Interpreting cost-effectiveness ratios in a cost-effectiveness analysis of risk-tailored prostate screening: A critique of Callender et al.

Incremental analysis of risk threshold adjustment

Callender et al.’s¹ cumulative assessment of the ratio of total costs to total QALYs as the risk threshold is relaxed means the analysis initially includes those men at highest risk who are likely the most cost-effective to screen and then progressively adds those of lower risk that are probably less cost-effective to screen. This cumulative approach to assessing the ratio of total costs to health effects hides the marginal effect of progressively relaxing the risk threshold to include lower risk screenees. The appropriate approach is to examine the incremental change in costs and health effects as the risk threshold is relaxed. Such an incremental analysis identifies what additional health gain is achieved at what additional cost of relaxing the risk threshold relative to the previous, more restrictive threshold.

Reinterpreting the results using an incremental approach indicates that relaxing the risk threshold is less cost-effective than appears under Callender et al.’s¹ cumulative analysis. The difference between the cumulative and incremental appraisal is shown in Figure 1. It plots the estimated costs and effects of the 17 precision screening strategies from Callender et al.’s¹ analysis. The least costly strategy is for the most conservative risk threshold of 10y-AR of 10%, while the most costly is for the least restrictive 2% 10y-AR threshold. The solid grey line shows the ratio of incremental costs and effects between the risk subgroups. The incremental ratios rise as the risk threshold falls and more men are screened. Beyond a certain threshold total effectiveness falls, implying that some screening becomes harmful to health. That is, it appears that reducing the risk threshold beyond a certain point harms at least some men.

Figure 1. Cost-effectiveness plane demonstrating the difference between cost-effectiveness ratios calculated on a cumulative and incremental basis.

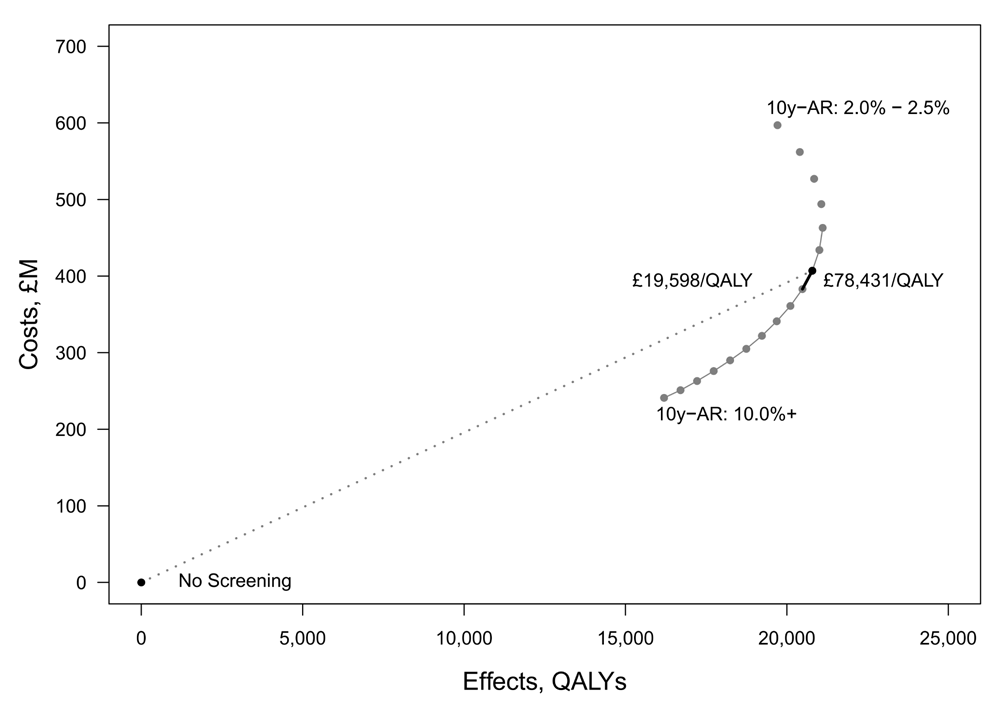
The dotted line in Figure 1 corresponds to the cumulative ratio reported in the by Callender et al.¹ as an ICER. In this case, corresponding to screening all men with a 10y-AR of at least 5%, which Callender et al.¹ report to be £19,598/QALY. The ratio of the incremental difference of screening men with a 10y-AR of 5.0–5.5% compared to men with a 10y-AR of 5.5% and above is £78,431/QALY. This ratio is shown in Figure 1 as the single thick black segment of the line joining the strategies. Further detail on the estimate is given in Table 1. It includes the ratios reported Callender et al.¹ as ICERs (“Reported ICERs”) and an additional cost-effectiveness ratio (CER) calculated as the incremental difference in costs and effects as the risk threshold is incrementally relaxed from 10y-AR of 10% to 2% (“Calculated CERs”). These CERs rise from £14,881/QALY for the highest risk men to £281,553/QALY for men with 10y-AR of 4.0–4.5%. There is no meaningful CER to report below a 10y-AR of 4% once the incremental change in QALY estimates becomes negative.

The policy significance of the difference between the cumulative and incremental analysis can be seen in the context of the UK cost-effectiveness threshold of £20,000/QALY as referenced by Callender et al.¹. Using the originally reported cumulative ratios, the first 11 risk thresholds would be considered cost-effective, as their reported ICERs are within the threshold (shown in italics in Table 1). Using the appropriate incrementally calculated CERs however, only the two most restrictive risk categories fall within the threshold (shown in bold). Accordingly, far fewer men appear cost-effective to screen than originally reported. Furthermore, those screened would start at an older age.

As an aside, it is useful to see how my interpretation of the results presented here is supported by the net monetary benefit (NMB) analysis provided by Callender et al.¹ within a supplementary appendix to their study. The variation of NMB with the risk threshold is presented by them in Figure H (A). It shows that NMB is maximised only when the risk threshold is near its most restrictive around 9.5% to 10% 10y-AR. This contradicts Callender et al.’s¹ finding that a 10y-AR of 5% would be cost-effective, as NMB should be maximised at the optimally cost-effective strategy. The observed maximisation of NMB around 9.5% to 10% 10y-AR corresponds with the optimally cost-effective policy (within those simulated) when using the incremental interpretation presented here.

Non-mutually exclusive strategy comparisons

At this point, I now turn to consider can the reinterpreted CERs reported in Table 1 be used as a reliable guide to screening policy. The above critique draws on the long and widely recognised distinction between the average and incremental cost-effectiveness ratios that is reflected in CEA guidelines^2–6. Note, however, that I have not described the CERs in Table 1 as ICERs. This is because there are further complications with the incremental reinterpretation of CERs that means they still may not be considered true ICERs and so are not a suitable guide to policy. Moreover, the published results cannot be reinterpreted into ICERs.

The standard interpretation of an ICER is the incremental comparison of costs and effects of mutually exclusive strategies that lie on the efficient frontier of the cost-effectiveness plane⁷. The way the alternative policy choices are specified within Callender et al.’s¹ analysis means they fail to constitute mutually exclusive strategies. As mentioned above, the relaxation of the risk threshold simultaneously adds men of lower lifetime risk of disease to the pool of screened men and reduces the age at first screen for those already within the pool of screened men. Lowering the age of screening initiation in higher risk men is not mutually exclusive of extending screening to lower risk men.

The non-mutually exclusive strategies within Callender et al.¹ means the incremental CERs reported in Table 1 correspond to a mixture of different policy choices for men of different lifetime risk. For example, reducing the risk threshold will bring forward the age of first screening for men of high lifetime risk, while it may entail a shift from no screening to one or more screens for a man of lower lifetime risk. While both men may have an equal 10y-AR at the initiation of screening, the differences in both their lifetime risk and the number of lifetime screens they receive mean the policy choices will likely be of different cost-effectiveness. There is no way to disaggregate the published results into a form that would permit policy makers to understand how large any differences in cost-effectiveness may be between men of different lifetime risk or identify what the optimal policies would be.

The implication of non-mutually exclusive strategies for policy is that although most of the incremental CERs in Table 1 are above the cost effectiveness threshold, it is not necessarily the case that all the corresponding policies are cost-ineffective. For instance, advancing the age at first screening for a man with a high lifetime risk might be less cost-effective than providing one lifetime screen at age 69 to a lower risk man. Accordingly, it would be premature to base policy on the incrementally interpreted CERs I present in Table 1.

To generate mutually exclusive policies within a single analysis, the authors should have held screening intensity constant for all but one sub-group at a time while varying intensity for the remaining sub-group. This policy generation process would have to be repeated for all sub-groups over all alternative strategies considered, resulting in a very large number of mutually-exclusive strategies. A much simpler alternative would be to model the range of screening strategies in separate analyses for each sub-group according to their lifetime risk.

If Callender et al.’s¹ analysis were to disaggregate men of different lifetime risks as described, then it would be possible to assess the different simulated screening strategies in each risk subgroup. That would allow the analysis untangle the differences of intensifying screening in higher risk men from extending screening to lower risk men. Such disaggregation is particularly important when we consider that the reduction in the risk threshold is eventually estimated to harm health. It is important to know which men are harmed by what intensity of screening.

Screening intensity and ICERs

The third issue of ratio interpretation considered here relates to the range of alternative comparator strategies required to adequately estimate ICERs. ICERs give the ratio of the incremental difference in costs to effects between one strategy relative to the next most effective relevant comparator strategy⁷. For example, the appropriate ICER estimation for a given strategy would typically require comparison to a less intense screening strategy with a lower number of lifetime screens, achieved by comparison to a strategy with either a longer interval or a narrower screening age range^3,7.

Previous prostate cancer screening CEAs demonstrate the relevance of incremental comparisons between alternative screening frequencies and varied screening age ranges. Heijnsdijk et al. show how ICERs rise as the number of lifetime screens increases⁸. While that analysis did not differentiate between risk strata, it does illustrate the relevance of including low intensity strategies as comparators to other strategies with shorter intervals and wider age ranges. They found that in an average risk population in a Dutch context the optimal strategy would be three screens per lifetime at ages 55, 57 and 59. They found no strategy with screening beyond age 59 to be cost-effective, indicating the relevance of considering alternative stopping ages in the case of prostate screening.

This context of previous research and well-established methods guidance tells us that even if Callender et al.’s¹ results can be disaggregated into mutually exclusive strategies for separate sub-groups according to lifetime risk, the resulting ratios would still only represent incremental changes to the start age of screening. Ideally, we would like to estimate a range of screening intensities in each sub-group, varying not only the screening start age, but also screening interval and, importantly, the screening stop age. In particular, we would be interested in the potential for low intensity screening to offer at least some prevention to the lowest risk men.

Modelling a wide variety of strategies intervals typically requires simulation of the natural history of disease and the imposition of stage-specific estimates test performance characteristics. Not all models are such "deep" models⁹. Callender et al.’s¹ analysis apparently is not one such model and may be restricted to the simulation of quadriennial screening intervals used in the trial that informed the model. While analyses limited to the simulation of one screening interval alone may come with the limitations of not being able to estimate a complete ICER on the basis of a comprehensive set of comparator strategies, these limitations are traded off against the advantage of less reliance on assumptions and reduced parameter uncertainty. There is no clear answer on the optimal balance in this trade-off when informing policy. Nevertheless, results from analyses without a complete set of comparators can still be useful to policy makers. CERs from analyses with a limited set of strategies that exceed the cost-effectiveness threshold can usefully rule out strategies as cost-ineffective. This is because any strategy with a CER exceeding the threshold within a limited set of comparators can never be cost-effective within a more complete analysis.

It is important to note that Callender et al. did clearly acknowledge the relevance of strategies of alternative age ranges and screening frequencies, but explained the data to support a risk stratified analysis was lacking. Accordingly, while the policy choices they simulated may not be those optimal relative to our theoretical understanding of optimally tailored strategies, the latter are, as yet, unsupported by data. Moreover, we should point towards the usefulness of Callender et al.’s analysis in informing further research. Their study concludes by stating prospective randomised controlled trials are required to better inform optimal policy. Further analysis of their model could usefully indicate what strategies would be most useful to compare and which parameters estimates are the priority to refine.